이제 비선형 구조의 자료구조들에 대해 정리해볼 시간이다.
비선형 자료구조

비선형 자료구조는 선형 자료구조와 달리 하나의 자료 뒤에 여러개의 자료가 존재할 수 있는 것이다.
트리나 그래프를 생각해보면 이해되는 듯!
즉, 자료들 간의 앞뒤 단계가 1:n, 또는 n:n의 관계이다.
그렇기 때문에 계층적인 구조를 나타내기에 적절하다.
그래프
그래프는 위의 그림과 같이 연결되어 있는 원소간의 관계를 표현한 자료구조이다!
이때 연결한 객체인 정점(Vertex)와 연결하는 간선(Edge)의 집합으로 구성된다.
- G = (V,E) → V는 정점들의 집합, E는 간선들의 집합
그래프 종류
무방향 그래프
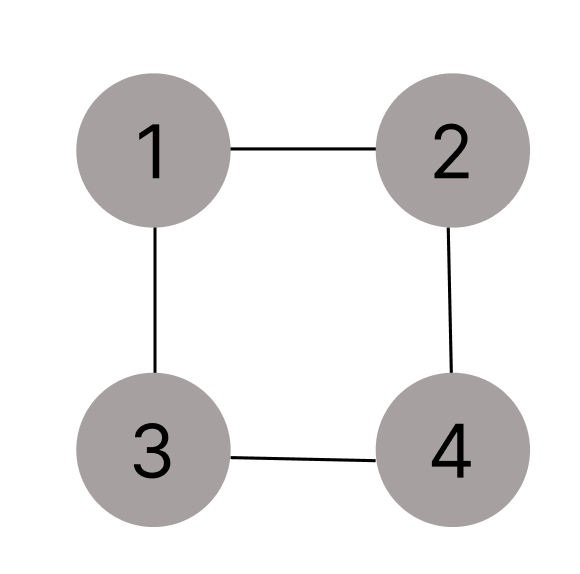
위의 그림과 같이 두 정점을 연결하는 간선에 방향이 없는 그래프!
무방향 그래프에서는 정점 Vi와 정점 Vj를 연결하는 간선을
(Vi, Vj)로 표현한다.
방향이 없기 때문에 결과적으로 (Vi, Vj) == (Vj, Vi)가 된다.
정점 V → {1,2,3,4}
간선 E → {(1,2),(1,3),(2,4),(3,4)}
방향 그래프

두 정점을 연결하는 간서에 방향이 존재하는 그래프!
방향 그래프에서는 정점 Vi와 정점 Vj를 연결하는 간선을
<Vi, Vj>로 표현한다.
무방향 그래프와 달리 <Vi, Vj> ≠ <Vj,Vi>
정점 V → {1,2,3,4}
간선 E → {<1,2>,<2,1>,<1,3>,<3,1>,<3,4>,<4,3>,<2,4>,<4,2>}
완전 그래프

완전 그래프는 한 정점에서 다른 모든 정점과 연결되어 최대 간선 수를 갖는 그래프이다.
위의 방향 그래프, 무방향 그래프 그림 모두 완전 그래프이다.
무방향 그래프 최대 간선수 → n(n-1)/2
방향 그래프 최대 간선수 → n(n-1)
부분 그래프

부분 그래프는 기존의 그래프에서 일부 정점이나 간선을 제외하여 만든 그래프이다.
가중 그래프

정점을 연결하는 간선에 가중치를 할당한 그래프이다!
유향 비순환 그래프

방향 그래프인데 사이클이 없는 그래프
사이클이 없는 그래프를 비순환 그래프라고 한다.
사이클 → 특정 정점에서 출발하여 간선과 정점들을 지나서 다시 출발한 정점으로 돌아오게 되는 것을 사이클이라고 한다!
연결 그래프

떨어져 있는 정점 없이 모두 간선에 의해 연결되어 있는 그래프를 말한다.
단절 그래프
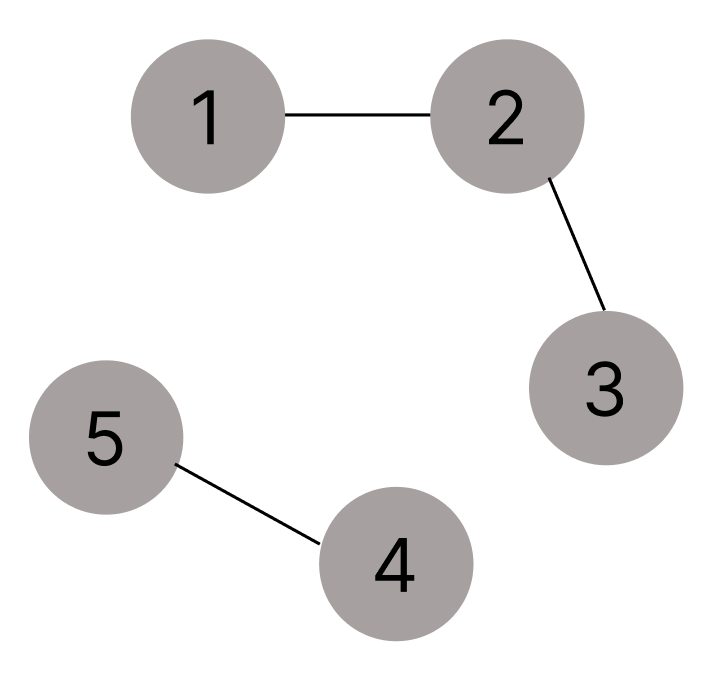
연결 그래프와 달리 연결되지 않은 정점이 있는 그래프를 말한다.
그래프 용어
인접한다 : 두 정점 Vi와 Vj가 연결되어서 간선 (Vi, Vj)가 있을 때 이를 인접한다라고 함.
부속된다 : 간선(Vi, Vj)는 정점 Vi와 Vj에 부속되어있다고 한다.
정점의 차수 : 무방향 그래프에서 하나의 정점에 인접한 정점의 수
진입 차수 : 방향 그래프에서 정점으로 들어오는 간선의 수
진출 차수 : 방향 그래프에서 정점에서 나가는 간선의 수
경로 : 정점 Vi에서 정점 Vj까지 간선으로 연결된 정점을 순서대로 나열한 리스트
단순 경로 : 모두 다른 정점으로 구성된 경로
경로 길이 : 경로를 구성하는 간선의 수
그래프의 특징
self-loop 뿐만이 아니라 loop/circuit 모두 가능하다.
계층의 개념이 아님 → 트리와의 차이
사이클이 있거나(순환) 사이클이 없거나(비순환)임.
그래프 구현 방법
그래프의 구현에는 인접 리스트 또는 인접 행렬로 구현이 가능하다.
인접 리스트
그래프의 노드를 리스트로 표현해 관계를 설정하는 것!

다음과 같은 그래프가 있다면
//0번 인덱스 제외
list = [[],[2],[1,3],[2],[5],[2,4]]
아래와 같이 표현이 가능하다.
특징
한 정점에 인접한 정점을 쉽게 찾을 수 있음! → 그 해당하는 정점의 인덱스로 확인만 하면 되기 때문
그래프에 존재하는 모든 간선의 수는 O(V+E) 안에 알 수 있음!
또한 필요한 만큼 공간을 사용하기 때문에 인접행렬에 비해 공간의 낭비가 적다.
하지만 두 정점이 연결되어 있는지 확인하기 위한 방법은 인접 행렬에 비해 시간이 오래 걸린다.
인접 행렬
마찬 가지로 위의 그래프가 있다면
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 2 | 1 | 0 | 1 | 0 | 0 |
| 3 | 0 | 1 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 1 |
| 5 | 0 | 1 | 0 | 1 | 0 |
다음과 같이 연결되어 있다면 1, 연결되지 않았다면 0으로 나타낸다.
특징
두 정점이 연결되어 있는지 조회하는데는 O(1)의 시간 복잡도를 가진다.
하지만 모든 정점에 대한 간선 정보를 입력해야 하기 때문에 인접 행렬 생성시 O(V^2)의 시간 복잡도가 소요된다.
공간의 낭비가 인접 리스트에 비해 크다.
'Basic > 자료구조' 카테고리의 다른 글
| [자료구조] 트리(tree) (0) | 2024.06.10 |
|---|---|
| [자료구조] 덱(Deque) (0) | 2024.05.07 |
| [자료 구조] 스택 & 큐 (0) | 2024.04.15 |
| [자료 구조] 연결 리스트 (0) | 2024.02.13 |
| [자료 구조] 배열 & 동적 배열 (0) | 2024.02.06 |
